نظريات في هندسة الدائرة
نظرية : مماس الدائرة في نقطة ما عليها يكون عمودياً على نصف القطر المار بنقطة التماس أو نصف قطر الدائرة يكون عمودياً على مماس الدائرة عند نقطة التماس .
- عكس النظرية : المستقيم العمودي على نصف القطر في دائرة عند نهايته يكون مماساً للدائرة .
نظرية : المماسان المرسومان للدائرة من نقطة مفروضه خارجها متساويان .

نظرية : إذا رسم من نقطة خارج دائرة مماس للدائرة وقاطع لها فإن : مربع طول المماس = حاصل ضرب القاطع بتمامه في جزئه الواقع خارج الدائرة .
( هـ و )2 = هـ جـ × هـ و
نظرية : مجموع كل زاويتين متقابلتين في الشكل الرباعي الدائري = 180 .
عكس النظرية : إذا كان مجموع الزاويتين المتقابلتين في الشكل الرباعي 180 كان هذا الشكل رباعياً دائرياً .
نظرية : الزاوية الخارجة عن الشكل الرباعي الدائري تساوي الزاوية المقابلة للمجاورة لها .
نظرية : الزاوية المماسية المحصورة بين مماس الدائرة وأي وتر فيها ما رنقطة التماس في إحدي جهتي الوتر تساوي الزاوية المحيطية المرسومة على هذا الوتر في الجهة الأخرى .

نظرية : كل ثلاث نقاط ليست على استقامة واحدة تمر بها دائرة واحدة نتيجة : نقطة تقاطع الأعمدة المنصفة لأضلاع المثلث ( محاور) هي مركز الدائرة الخارجة للمثلث.

نظرية
قياس الزاوية المحيطية يساوي نصف قياس الزاوية المركزية المشتركة معها في القوس . وبصورة آخرى قياس الزاوية المركزية = ضعف قياس الزاوية المحيطية .
- نتيجة: الزوايا المحيطية المشتركة في قوس واحد متطابقة .

قصة منشئ الأرقام العربية والمنتشرة عند الغرب اليوم

 

قام الخوارزمي قام بتأليف أرقام أخرى

 تُعرف اليوم بإسم الأرقام العربية عند الغرب ..

 ولم تكن تحظ بإنتشار واسع عند العرب .. 

ولكنها إنتشرت فيما بعد في الأندلس والمغرب العربي ..

 ومن هناك إنتشرت في أوربا وفي جميع أنحاء العالم ..

لأنها أفضل من الحروف التي تدل على قيم رقمية لدى أوربا في ذلك الزمان لصعوبة التعامل معها

قام الخوارزمي بتصميم الأرقام العربية حسب أعداد الزوايا لكل رقم .. وهي تتمثل بالأشكال التالية :

الرقم واحد .. زاوية واحدة

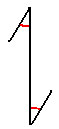
الرقم إثنان .. زاويتان

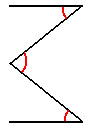
الرقم ثلاثة .. ثلاث زوايا

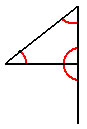
الرقم أربعة .. أربع زوايا

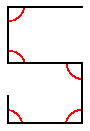
الرقم خمسة .. خمسة زوايا

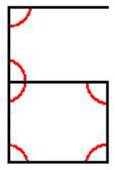
الرقم ستة .. ستة زوايا

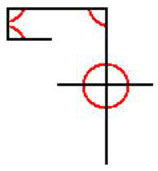
الرقم سبعة .. سبعة زوايا

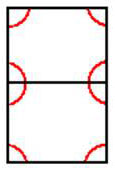
الرقم ثمانية .. ثمان زوايا

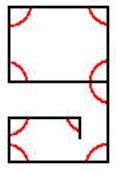
الرقم تسعة .. تسعة زوايا

وأخيرا .. الرقم صفر .. لا توجد أي زاوية

ثم دخلت بعض التعديلات على هذه الأشكال .. حتى صارت بالأشكال المعروفة حالياً !

* غدير الروقي 

عمليات حسابية غريبة جداً !

الاولـــــــى 

فكر برقم و اكتبه على ورقة

اضف 2 على الرقم الذي أخترته

أضرب الناتج في 4

أقسم الناتح إلى نصفه

أنقص من الناتج 4

أقسم الناتج على الرقم الاول الذي اخترته

الجواب سيكون ( 2)

الثانيــــة  

 اختار رقم ما بين 1- 10 اكتبه علي ورقه 

اضرب الرقم في 6 

  أضف 4 الي الناتج 

 اقسم الناتج على 2 

 انقص 2 من الناتج 

 اقسم الناتج على 3 

 جوابك سيكون الرقم الذي اخترته من الاول

 الثالثـــة 

 فكر برقم و اكتبه على ورقه 

اضف 5 علي الرقم اذي اخترته 

 اضرب الناتج في 5 

 انقص 25 من الناتج 

 اقسم الناتج علي الرقم الاول الذي اخترته 

( انت بقيت معاك (  5

* غدير الروقي 

علم الصيدله عند المسلمين

ابن سينا :

أبو علي الحسين بن سينا ، من أبرز علماء المسلمين العاملين في مجال الطب والعلاج ، ولد في "خرميش" إحدى قرى "بخارى" عام 370 هـ/ أغسطس 908م ، رحل إلى جرجان وهو في العشرين من عمره وبعد وفاة والده ، وأقام فيها ، وألف كتابه "القانون في الطب"، ولكنه ما لبث أن رحل إلى همذان فحقق شهرة كبيرة ، وصار وزيرا للأمير "شمس الدين البويهي"، إلا أنه لم يطل به المقام هناك ، إذ رحل إلى أصفهان وحظي برعاية أميرها وظل فيها حتى وافته المنية عام 428 هـ / 1037م. 

يعد كتابه " القانون في الطب " من أشهر المؤلفات الطبية التي سجلها التاريخ، وظلت هذه الموسوعة مرجعاً للأطباء والصيادلة في كثير من بلاد العالم المتحضر، حتى أوائل القرن الثامن عشر، ولقد بدأت كتبه تترجم منذ أوئل القرن الثاني عشر، وذلك بعض دارساته أساساً لبرامج التعليم الطبي والصيدلي في إسبانيا وفرنسا وإيطاليا حتى النصف الأول من القرن الثامن عشر. 

وكان لابن سينا معرفة جيدة بالأدوية وفعاليتها، وقد صنف الأدوية في ست مجموعات، وكانت الأدوية المفردة والمركبة " الأقرباذين" التي ذكرها في مصنفاته وبخاصة كتاب القانون لها أثر عظيم وقيمة علمية كبيرة بين علماء الطب والصيدلة، وبلغ عدد الأدوية التي وصفها في كتابه نحو 760 عقَّارًا رتبها ألفبائيا. 

ومن المدهش حقا أنه كان يمارس ما يعرف بالطب التجريبي ويطبقه على مرضاه، فقد كان يجرب أي دواء جديد يتعرف عليه على الحيوان أولا، ثم يعطيه للإنسان بعد أن تثبت له صلاحيته ودقته على الشفاء. 

كما تحدث عن تلوث البيئة وأثره على صحة الإنسان فقال: "فما دام الهواء ملائما ونقيا وليس به أخلاط من المواد الأخرى بما يتعارض مع مزاج التنفس، فإن الصحة تأتي. وذكر أثر ملوثات البيئة في ظهور أمراض حساسية الجهاز التنفسي.

جابر بن حيان:

هو أبو عبد الله جابر بن حيان بن عبد الله الكوفي المعروف بالصوفي. ولد في طوس " خراسان" وسكن الكوفة، حيث كان يعمل صيدلانياً وكان أبوه عطاراً . بنسبته الطوسي أو الطرطوسي، وينحدر من قبيلة الأزد. ويقدّر الزمن الذي ولد فيه جابر بين 721 م – 722 م، أما تاريخ وفاته فغير معروف تماما. ويقال أنه توفي سنة 200 هـ أو ما يوافق 815 م . ويقول هولميارد Holmyard أن جابر عاش ما يقارب 95 سنة، ودليله في ذلك أن المؤلفات التي ألّفها لا يمكن إنجازها بأقل من هذا الزمن 

يُعد جابر بن حيّان علم من أعلام العرب العباقرة ، وأول رائد للكيمياء ، وقد أيّد هذه الحقيقة أبو بكر الرازي، عندما كان يشير إلى جابر في كتبه فيقول "أستاذنا" . تقدم علم الكيمياء تقدماً عظيماً على يده ، فهو أول من حضّر حامض الكبريتيك، وحامض النيتريك، وكربونات الصودا، وكربونات البوتاسيوم، وماء الذهب. وهو أيضاً أول عالم كيميائي استعمل الموازين الحساسة في التجارب الكيميائية، وأول من ابتدع عمليات البلورة، والترشيح، والتقطير، والتصعيد وغيرها. 

ومن أقواله : " إن من واجب المشتغل في الكيمياء، العمل وإجراء التجارب، وإن المعرفة لا تحصل إلا بها" وبهذا يكون جابر بن حيان ، ومن بعده مسلمة بن أحمد المجريطي قد سبقا علماء الغرب بعدة قرون في إخضاع العلم للتجربة، ووضع أسس المنهج العلمي الذي يقوم على التجربة. 

من مؤلفاته في الكيمياء والصيدلة كتاب " الموازين" وكتاب " سر الأسرار" وكتاب "الخواص" وكتاب " السموم ودفع مضارها" ولقد ترجمت معظم كتبه إلى اللغات الأوربية, وظلت مرجعاً في جامعات أوربا لعدة قرون. 

الجوهره اليوسف

عالم الرياضيات فيثاغورس

فيثاغورث أو فيثاغورس أوفيتاغورس الساموسي هو فيلسوف ورياضي إغريقي (يوناني) عاش في القرن السادس قبل الميلاد، وتنسب إليه مبرهنة فيثاغورث.

تحاك حول شخصية بيتاغوراس العديد من الروايات والأساطير ويصعب التحقق منها حيث يروى أن بيتاغوراس الساموسي ولد في جزيرة ساموس على الساحل اليوناني. في شبابه قام برحلة إلى بلاد ما بين النهرين ( سوريا والعراق حاليآ ) وأقام في منف بمصر . وبعد 20 سنة من الترحال والدراسة تمكن بيتاغوراس من تعلم كل ما هو معروف في الرياضيات من مختلف الحضارات المعروفة آنذاك. لكن حالما عاد بيتاغورث إلى مسقط رأسه اضطر للفرار منه وذلك لمعارضته للدكتاتور بوليكراتس في ما يخص الإصلاحات الاجتماعية. في حوالي 523 ق م، استقر بيتاغورث في جنوب إيطاليا في كروتوني حيث تعرف على شخص يدعى ميلان وكان من أغنياء الجزيرة فقام ميلان بمساعدة بيتاغوراس ماديا. في هذه الأثناء ذاع صيت بيتاغوراس واشتهر إلا أن ميلان كان أشهر منه آنذاك حيث كان عظيم الجثة، وحقق 12 فوزا في الألعاب الأولمبية، الشيء الذي كان رقما قياسيا آنذاك. كان ميلان مولعا بالفلسفة والرياضيات بالإضافة للرياضة، وبسبب ولعه هذا وضع قسما من بيته في تصرف بيتاغورس كان يكفي لافتتاح مدرسة.

اهتم اهتماما كبيرا بالرياضيات وخصوصا بالأرقام وقدس الرقم عشرة لأنه يمثل الكمال كما اهتم بالموسيقى وقال أن الكون يتألف من التمازج بين العدد والنغم. أجبر فيثاغورث أتباعه من دارسي الهندسة على عدة أمور قال أنه نقلها في رحلاته من المزاولين للهندسة:

ارتداء الملابس البيضاء 

التأمل في أوقات محددة. 

الامتناع عن أكل اللحوم 

الامتناع عن أكل الفول. 

يعتقد فيثاغورس وتلاميذه أن كل شيء مرتبط بالرياضيات وبالتالي يمكن التنبؤ بكل شيء و قياسه بشكل حلقات إيقاعية.

استطاع فيثاغورس إثبات نظريته مبرهنة فيثاغورث في الرياضيات والتي تقول: في مثلث قائم الزاوية، مربع طول الوتر يساوي مجموع مربعي طولي الضلعين المحاذيين للزاوية القائمة، عن طريق حسابه لمساحة المربعات التي تقابل كل ضلع من أضلاع المثلث قائم الزاوية. استفاد الكثير من المهندسين في العصر الحاضر من هذه النظرية في عملية بناء الأراضي. ((لمعرفة المزيد حول هذه النظرية انتقل إلى مبرهنة فيثاغورس)).    

الجوهره اليوسف 

علم حساب المثلثات

علم حساب المثلثات

مقدمة
إن الرياضيات بفروعها المختلفة قد ساعدت الإنسان منذ القدم وحتى وقتنا الحاضر في دراسة وتحليل العلاقات بين الظواهر الطبيعية المختلفة وبالتالي في التعرف على بعض القوانين التي تحكم الكون المليء بالأسرار ولقد اخترت موضوع بحثي عن حساب المثلثات
فحساب المثلثات هو علم عربي إسلامي، ويعترف جميع علماء الرياضيات الأوربيين بأن المسلمين أسهموا الإسهام الأساسي في إنشاء علم المثلثات، وأن الفضل يرجع لهم في جعله علمًا منتظمًا ومستقلا عن علم الفلك،
تحدثنا بشكل موجز عن حساب المثلثات دعونا نتحدث بشيء من التفصيل

نبذة تاريخية

يعود تاريخ حساب المثلثات إلى أقدم ما دون عن الرياضيات في مصروبابل، حيث قاس البابليون الزوايا بالدرجات والدقائق والثواني. وحتى عصراليونانيين، لم يوجد أي تطور ملحوظ في حساب المثلثات،
وفي القرن الثاني قبلالميلاد، وضع الفلكي هيباركوس جدول مثلثي لحل المثلثات، حيث بدأ بــ 7.5ْ حتى وصلإلى 180ْ بدرجات مقدارها 7.5ْ، وقد أعطى الجدول لكل زاوية طول الوتر المقابل لهذهالزاوية في دائرة ذات نصف قطر ثابت ر. ومثل هذا الجدول مكافئ لجدول الجيب ، ولم تكنالقيمة التي استخدمها هيباركوس لنصف القطر (ر) محددة، ولكن بعد مضي 300 عام استخدمالفلكي بطليموس (ر)= 60 لأن اليونانيين قد أخذوا نظامالأرقامالستينية البابلي.
تلخيص لبعض قوانين حساب المثلثات
1- ظاس = جاس/ جتاس
2-ظتاس = 1 / ظاس ...... ظتاس = جتاس/ جاس
3- قاس= 1/ جتاس
4- قتاس = 1/ جاس
5- جا^2س+جتا^2س=
6- قا^2س=1+ظا^2س
7- قتا^2س=1+ظتا^2س
8- جا( - س) = - جاس
9- جتا( - س) = جتاس
10- ظا( - س) = - ظاس

العلماء المسلمين الذين ساهموا في علم حساب المثلثات
ابن سنان البتاني، وهو أول من استعمل المعادلات المثلثية، وأبو الوفاء البوزجاني أول من أدخل المماس في عداد النسب المثلثية، واستخدم المماسات، والقواطع، ونظائرها في قياس المثلثات والزوايا. كما ابتكر طريقة لإنشاء جداول للجيوب في المثلثات المستوية، وأعطى جيب نصف الدرجة صحيحًا لثمانية أرقام عشرية، ووضع جداول لنسبة الظل التي أدخلها مع نسبتي القاطع وقاطع التمام.
أبو العباس التبريزي، وأبو جعفر الخازن في القرن الرابع الهجري، والبيروني، والعالم الأندلسي الجليل أبو إسحاق إبراهيم بن يحيى النقاش المعروف بابن الزرقالي عند الغربيين، وكان له أثر عظيم في علم حساب المثلثات وخاصة المثلث الكروي، ووجد اسم جيب الزواية واستعمالها في كتاب ابن الزرقالي. وقد ألف كذلك جداول لعلم حساب المثلثات ترجمها الغرب إلى اللاتينية. ويقول "سيديو" عن إنجازات البتاني في علم المثلثات: "يرجع أول تقدم في علم المثلثات إلى البتاني، فقد بدا لهذا الفلكي العظيم -الملقب ببطليموس العرب- أن يستبدل الأقواس بالأوتار للأقواس المضاعفة أي جيوب الأقواس المقترحة0
أقوال عن مساهمات العلماء المسلمين
قال "رام لاندو" في كتابه "المؤثر على حضارة العرب": "إن حساب المثلثات في أوربا كان مأخوذًا من علم حساب المثلثات عند المسلمين.
ويقول "ديفيد سميث" في كتابه تاريخ الرياضيات": "...ولم تدرس المثلثات الكروية المائلة بصورة جديدة وجدية إلا على أيدي العرب والمسلمين في القرن الرابع الهجري، العاشر الميلادي".
الخاتمة
في الختام لقد وصلنا الى نهاية موضوعنا الشيق الذي استفدت منه معلومات قيمة لم أكن اعرفها فقد علمت إن المسلمين لهم انجازات واسعة جدا في علم حساب المثلثات ولكم أردت إن يكون المسلمين اليوم كالمسلمين العلماء أصحاب الحكمة والذكاء والابتكار لا التقليد
وتعرفت على استخدام زوايا الارتفاع والانخفاض وما لها من اهمية توفير الوقت والجهد وإعطاء معلومات أكثر دقة
واختم بحثي بعبارة
(الرياضيات كالبحر بما فيها من معلومات)

نوف الصيخان

مكعب روبيك

مكعب روبيك

من منا لايعرف هذا المكعب العجيب الذي شدنا شكله لاقتنائه في طفولتنا ولكننا سرعان ما دخل الملل واليأس الى قلوبنا بعد محاولات الفشل العديدة !!!

كان حل هذا المكعب هاجس يراود عقولنا الصغيرة لنثبت بأننا الأذكى ... و للعدل فإننا تغلبنا على صعوبة هذا الحل بحيلتنا التي كانت اذكى وهي نزع ملصقات المربع ووضعها بمربع آخر فتتشابه ألوان الجهة الواحدة (:

ما أود قوله بـأن موضوع هذا المربع شغل عقلي كثيرا وكان من أوائل الموضوعات التي بحثت عنها كثيرا بداية دخولي عالم الانترنت وكان البحث ممتعا جداً ومما وجدت فيه بأن مخترع المكعب النحات الهنغاري وأستاذ العمارة إرنو روبيك سجل براءة اختراع وهو جدير بذلك ,, وقد حقق اشخاص كثيرون أرقاما قياسية لحل هذا المكعب .

إذاً حل هذا المكعب ليس بالمستحيل فبالتأكيد إنه صنع بآليه معينه وحله ايضا له آليه معينه وهو يعتمد على التباديل واللغوريتمات بشكل رئيسي !!

يوجد باليوتيوب طرق حل كثيرة (:

أطيب تحياتي هند القحطاني !!